Given a unbiased coin, can you model the Bernoulli distribution with any probability $p$?

Extra: How do we go back?

Fair coin to any coin

Assume that you only have access to an unbiased coin that shows head and tails each with a probability of $\frac{1}{2}$. Given a probability $p$ with $0 < p < 1$. I show you a neat trick on how to efficiently use your coin to model a random process with a resulting binary variable $Z$, so that $P(Z = 1) = p$. Of course, we want to keep the number of times $T$ that we throw the coin minimal in expectation.

The idea is quite simple. Using the $2$-adic (or binary) representation of $p$, we can write

$$ p = [0.p_1 p_2 p_3 \dots]2 = p_1/2 + p_2/4 + p_3/8 + \dots = \sum, $$ for $p_i \in {0, 1}$. For example $p = 1/3$ would be written as:}^\infty{\frac{p_i}{2^i}

$$ p = 1/3 = [0.01010101\dots]_2 = [0.\overline{01}]_2. $$

This can be checked by using the well known formula $\sum_{k \geq 0}{q^k} = \frac{1}{1 - q}$ for $0 < q < 1$: $$ [0.\overline{01}]2 = \frac{1}{4} + \frac{1}{16} + \frac{1}{64} + \frac{1}{256} + \dots = \sum - 1 = 4/3 - 1 = 1/3. $$}{\left( \frac{1}{4}\right)^k

The solution is to iterate through the digits of the $2$-adic representation after the decimal point and in each step throwing a coin:

• Head: proceed to the next digit.
• Tail: stop the process and output the value of the current digit $p_i$ as a result.

We denote $S$ as the sequence of coin tosses that happened in the process. It can be seen that the $i$-th digit after the decimal point gets selected with a probability of $1 / 2^i$ and the only sequence of the process that leads to this digit is $S = hh\dots ht = h^{i-1}t$ ($h$ denotes head, $t$ tails). This exactly gives us back $p$:

\begin{align} P(Z = 1) &= P(S = t, p_1 = 1) + P(S = ht, p_2 = 1) + \dots \ &= P(S = t) p_1 + P(S = ht) p_2 + \dots \ &= \frac{1}{2} p_1 + \frac{1}{4} p_2 + \dots \ &= [0.p_1 p_2 p_3 \dots]_2 = p. \end{align}

The number of steps $T$ the process requires is distributed via a geometric distribution with $q = 1/2$, thus $$ E[T] = 1/q = 2, $$ in conclusion we only expect to need two coin tosses to model the Bernoulli distribution with probability $p$.

Any coin to fair coin

The other way round is also a known trick. Given a coin which would appear with probability $p$ on head and $1-p$ on tail ($0 < p < 1$) we need to model a process $Z$ that outputs $0$ or $1$ with equal probability $\frac{1}{2}$.

We throw our fair coin twice and note the results $S = (S_1, S_2)$, then we go through each case as follows:

• $S = (h, t) \Rightarrow$ output $Z = 1$;

• $S = (t, h) \Rightarrow$ output $Z = 0$;

• $S = (h, h)$ or $S = (t, t)$ then throw again.

We can easily calculate that the probabilities of the first two cases are equal:

\begin{align} P(S = (h, t)) &= P(S_1 = h, S_2 = t) \ &= P(S_1 = h) P(S_2 = t) \ &= p(1-p) = (1-p)p \ &= P(S_1 = t, S_2 = h) = P(S = (t, h)). \end{align}

By induction it follows for any length $T$ of the process the two outcomes are equally like, thus must be $1/2$.

How many coin tosses do we need? For each step we need to toss two coins, so we need to look at twice the number of steps $T$ of the process. $T$ is distributed geometrically with probability of success $2p(1-p) = 1 - (p^2 + (1-p)^2)$. The mean amount of steps is thus $\frac{1}{2p(1-p)}$.

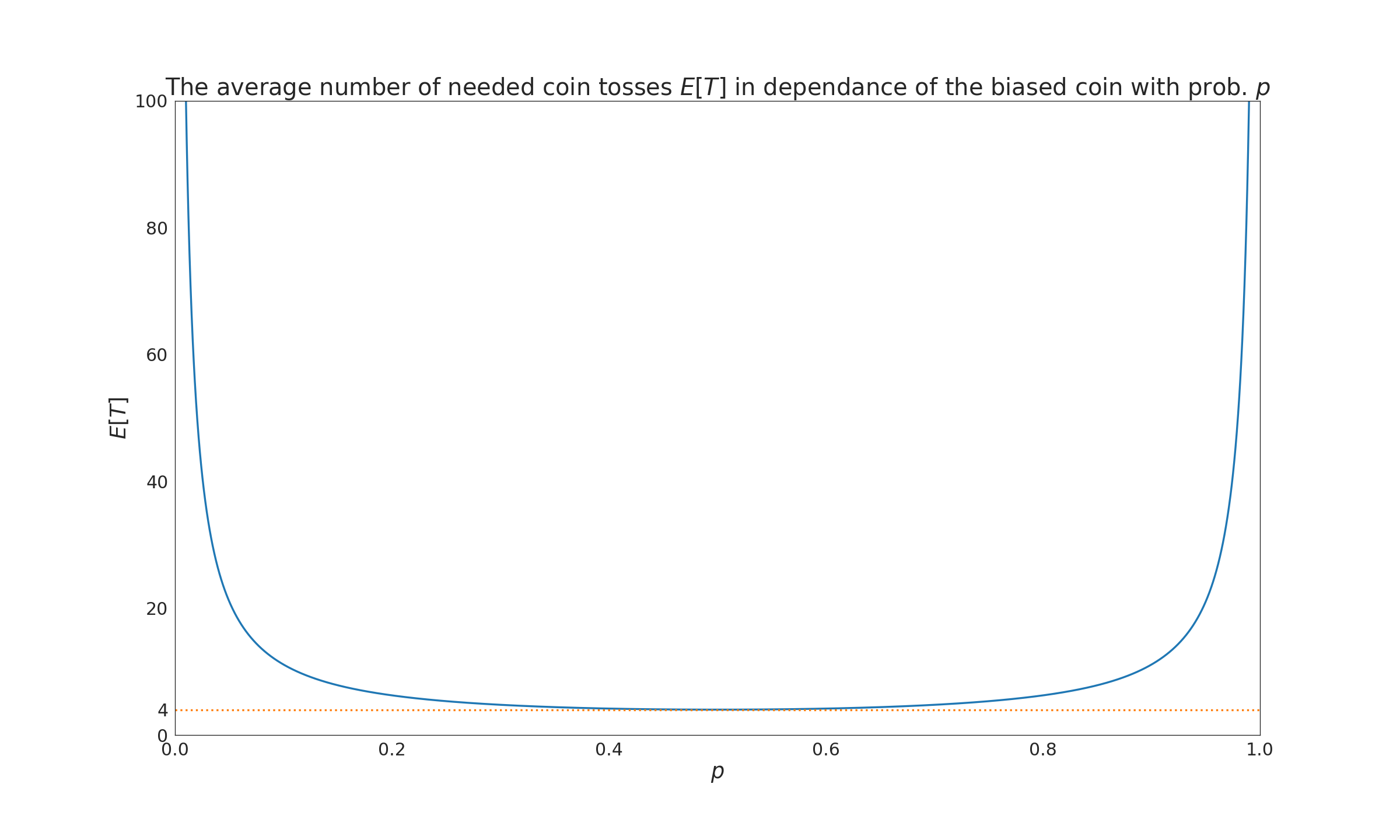
It can be seen that for most configurations of $p$ we need $4$ coin tosses (as the expected number of process steps/rounds are $2$). Around $p = \frac{8}{11}, \frac{3}{11}$ we start to require $5$ tosses on average. Obviously this “explodes” close to the boundaries as either heads or tails will keep be thrown requiring yet another round.